프로토타입 기반 군집(prototype-based clustering)
프로토타입 기반 군집은 각 클러스터가 하나의 프로토타입으로 표현된다는 뜻이다.
프로토 타입은 연속적인 특성에서는 비슷한 데이터 포인트의 센트로이드(centroid, 평균)이거나,
범주형 특성에서는 메도이드(medoid)(가장 대표되는 포인트나 가장 자주 등장하는 포인트)이다.
비지도 학습(unsuperviesed learning)의 군집 분석(clustering analysis)
k-평균(k-means)
k-평균은 군집 알고리즘 중 하나로 산업 현장이나 학계에서 널리 사용된다.
군집은 비슷한 객체로 이루어진 그룹을 찾는 기법이다.
한 그룹 안의 객체들은 다른 그룹에 있는 객체보다 더 관련되어 있다.
상용 애프리케이션의 문서나 음악, 영화를 여러 주제의 그룹으로 모으는 경우를 볼 수 있다.
또는 추천 엔진에서 하듯이 구매 이력의 공통 부분을 기반으로 관심사가 비슷한 고객을 찾는 작업에도 사용할 수 있다.
k-평균은 구현하기가 매우 쉽고 다른 군집 알고리즘에 비해 계산 효율성이 높기 때문에 인기가 많다.
k-평균 알고리즘은 프로토타입 기반 군집(prototype-based clustering)에 속한다.
k-평균 알고리즘은 원형 클러스트를 구분하는 데 뛰어나지만, 사전에 클러스터 개수 k를 지정해야 하는 단점이 있다.
(적절하지 않은 k를 선택하면 군집 성능이 좋지 못하다.)
엘보우 방법과 실루엣 그래프 등은 최적의 k를 결정하는데 도움이 된다.
간단한 2차원 데이터셋 생성
from sklearn.datasets import make_blobs
X, y=make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
150개의 포인트로 구성되어 있으며, 3개의 밀집된 그룹을 형성한다.
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()
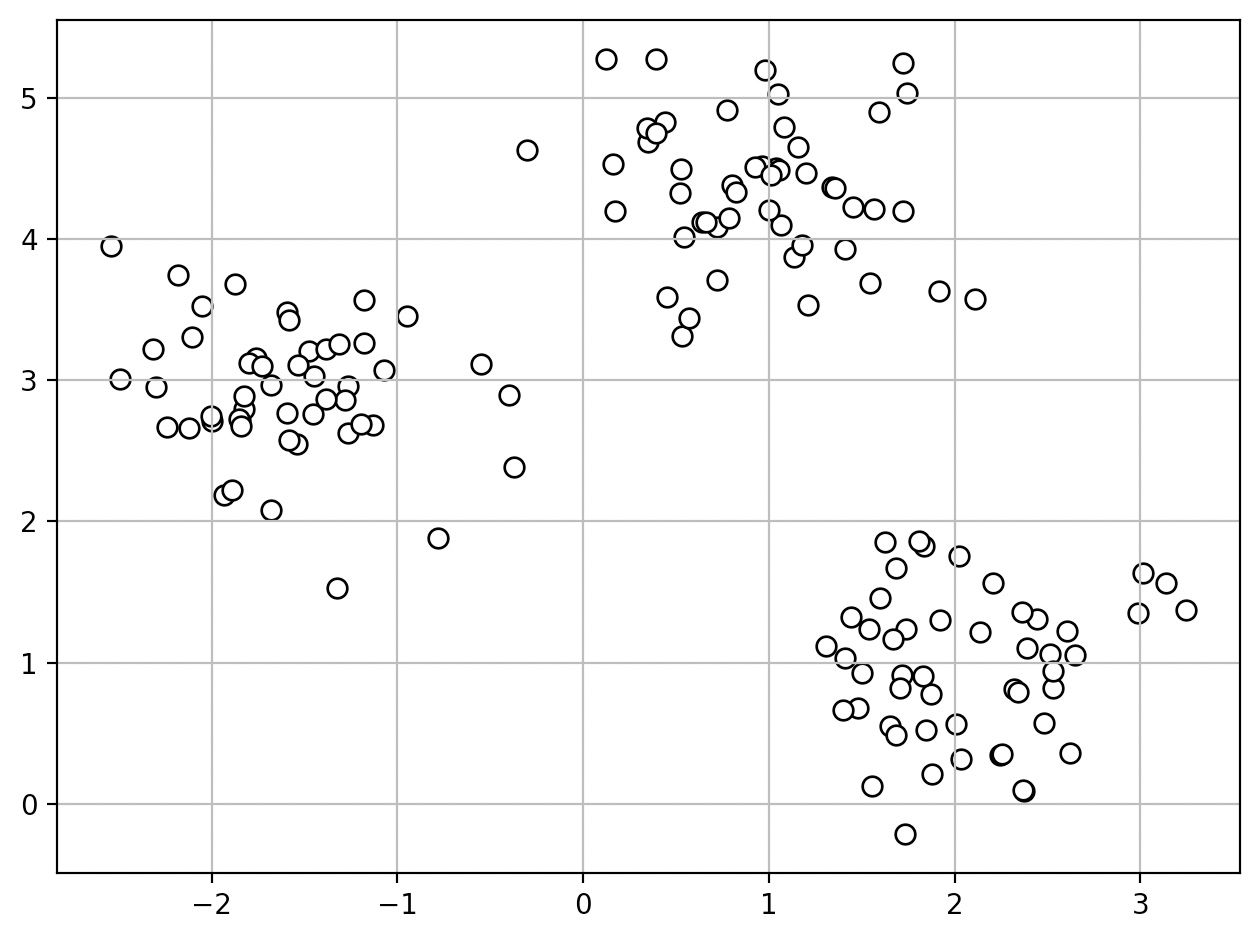
군집 애플리케이션, 비지도 학습의 목표는 특성의 유사도에 기초하여 샘플을 그룹으로 모으는 것이다.
process of k-means algorithm
1. 샘플 포인트에서 랜덤하게 k개의 센트로이드를 초기 클러스터 중심으로 선택
2. 각 샘플을 가장 가까운 센트로이드 miu, j(inluded in{l, …, k})에 할당한다.
3. 할당된 샘플들의 중심으로 센트로이드를 이동한다.
4. 클러스터 할당이 변하지 않거나 사용자가 지정한 허용 오차나 최대 반복 횟수에 도달할 때까지 단계 2와 3을 반복한다.
유사도는 거리의 반대 개념으로 정의할 수 있다.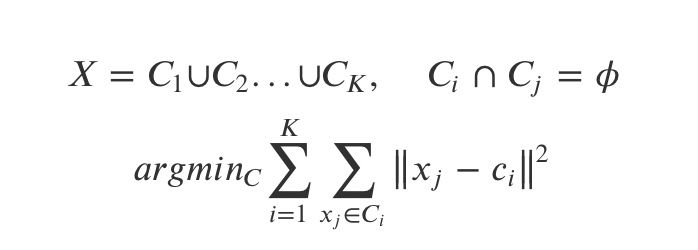
연속적인 특성을 가진 샘플을 클러스터로 묶는데 m-차원 공간에 있는 두 포인트 x와 y사이의
유클리디안 거리의 제곱(squared Euclidean distance)를 사용한다.
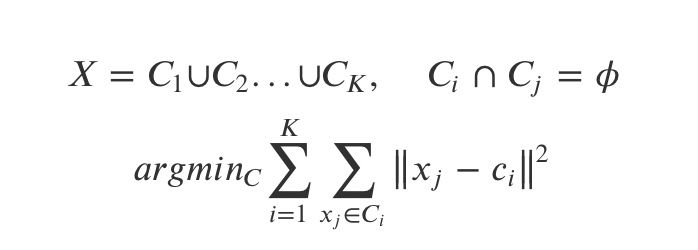
클러스트 내 제곱 오차합(SSE) 또는 클러스터 관성(cluster inertia)을 반복적으로 최소화
from sklearn.cluster import KMeans
km=KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km=km.fit_predict(X)
n_clusters=3: 클러스터 개수를 3개로 지정한다.
n_init=10: 랜덤하게 10번 시작 센트로이드를 정하고 SSE가 가장 낮은 모델을 선택한다.
tol은 수렴을 결정하는 클러스터 내 제곱 오차합의 변화량에 대한 허용 오차를 조정한다.
수렴에 문제가 있다면, tol의 값을 늘릴 수 있다.
(tol만큼 줄어들지 않으면 max_iter를 다 채우지 않았더라도 종료)
사이킷런에서는 만일 한 클러스터가 비어 있다면 빈 클러스트에서 가장 멀리 떨어진 샘플의 포인트에 센트로이드를 다시 할당한다.
k-평균 알고리즘을 유클리디안 거리 지표를 사용하여 실제 데이터에 적용할 때, 특성이 같은 스케일인지 확인할 것!
z-점수 표준화, 최소-최대 스케일 변환
plt.scatter(X[y_km==0, 0], X[y_km==0, 1], s=50, c='lightgreen', marker='s', edgecolor='black', label='Cluster 1')
plt.scatter(X[y_km==1, 0], X[y_km==1, 1], s=50, c='orange', marker='o', edgecolor='black', label='Cluster 2')
plt.scatter(X[y_km==2, 0], X[y_km==2, 1], s=50, c='red', marker='v', edgecolor='black', label='Cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', edgecolor='black', label='Centroids')
plt.legned(scatterpoinst=1)
plt.grid()
plt.tight_layout()
plt.show()
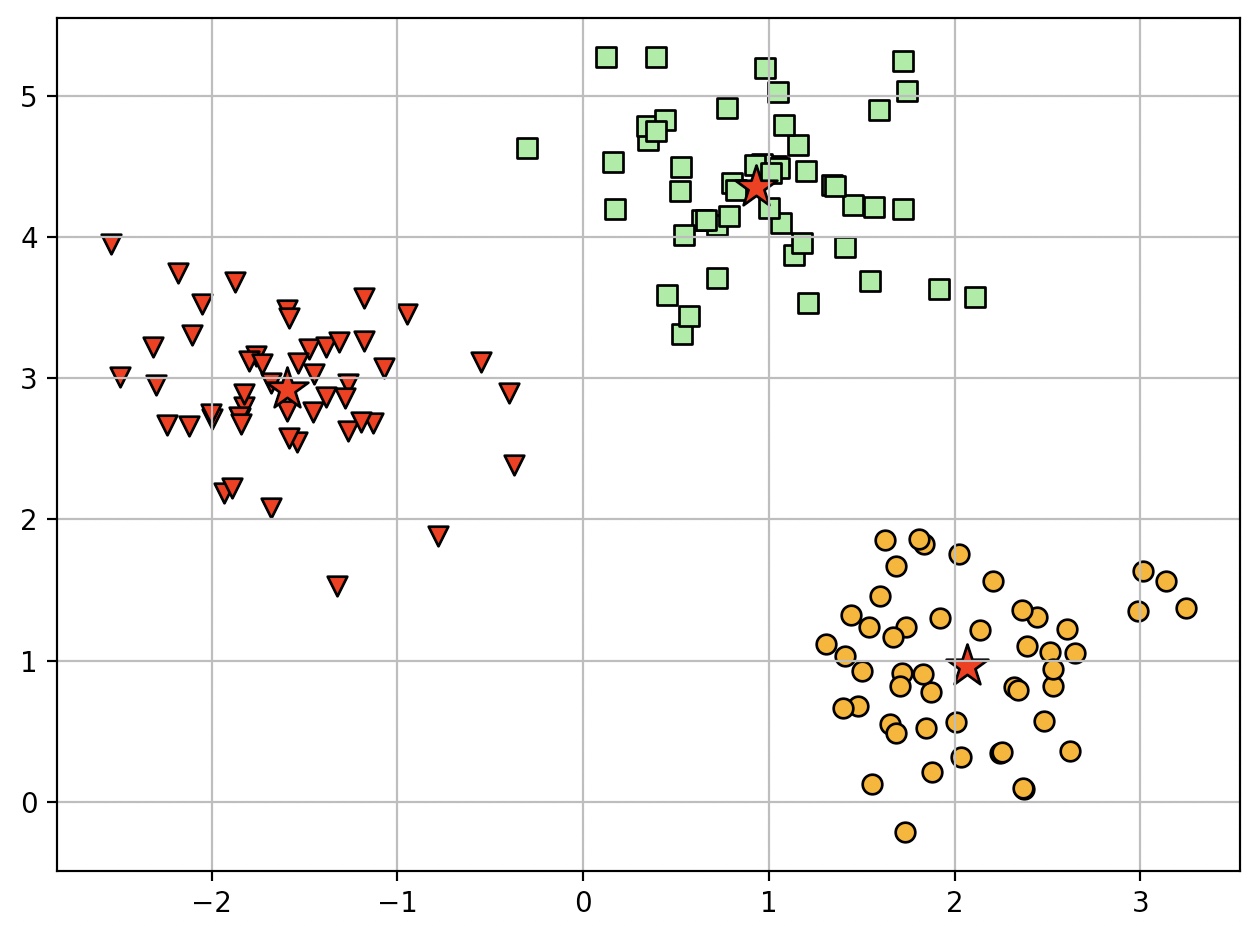
k-평균 알고리즘은 작은 데이터셋에서 잘 작동하지만, 클러스터 개수 k를 지정해 주어야 한다는 단점이 있다.
시각화 할 수 없는 고차원 데이터셋에서는 k를 사전에 명확하게 알기 어렵다.
k-평균은 클러스터가 중첩되지 않고 계층적이지 않다. 또한 각 클러스터에 적어도 하나의 샘플이 있어야 한다고 가정한다.
k-menas++는 k-means의 단점(처음 군집 갯수 지정)을 해결하지는 못하지만, 초기 센트로이드가 서로 멀리 떨어지도록 위치시키기 때문에
k-menas보다 일관되고 좋은 결과를 얻을 수 있다.
process of k-means++
1. 선택한 k개의 센트로이드를 젖아할 빈 집합 M을 초기화한다.
2. 입력 샘플에서 첫 번째 센트로이드를 랜덤하게 선택하고 M에 할당한다.
3. M에 있지 않은 각 샘플에 대해 M에 있는 센트로이드까지 최소 제곱 거리를 계산
4. 가중치가 적용된 확률 분포를 사용하여 다음 센트로이드를 랜덤하게 선택한다.
5. k개의 센트로이드를 선택할 때까지 단계 3과 4를 반복
6. k-평균 알고리즘을 수행한다.
from sklearn.cluster import Kmeans
Kmeans의 init 매개변수를 k-means++로 지정하면 k-평균++를 사용할 수 있다.(default 값이 k-means++이다.